Комплексные числа основные понятия

2.5. Основные сведения о комплексных числах
    Комплексным числом называется выражение вида
,                                                      (2.6)
где – обозначение комплексного числа; a и b – соответственно действительная и мнимая части комплексного числа; – мнимая единица.
    Величины a и b часто обозначают следующим образом: a = Re, b = Im. Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.

Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 2.8). Горизонтальная и вертикальная оси, отмеченные соответственно знаками + и +j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси.

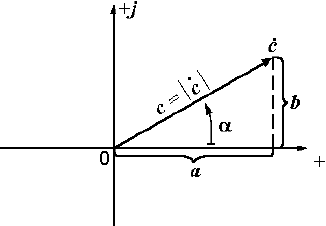
Image4924.gif (1690 bytes)
Рис. 2.8. Вектор на комплексной плоскости

На рис. 2.8 с = !! – модуль комплексного числа, равный длине вектора, а a = arg – аргумент комплексного числа. Так как а = c cos a , а
b = c sin a , то = c (cos a + j sin a ) – тригонометрическая форма комплексного числа. С помощью формулы Эйлера последняя преобразуется в показательную форму . Применяется еще и полярная форма , в самой простой форме задающая модуль и аргумент комплексного числа.

Свойства мнимой единицы (рис. 2.9):
, ,
,
,
и т.д.,
Image4905.gif (1249 bytes) .

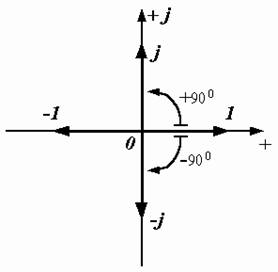Рис. 2.9. Единичный вектор
в комплексной плоскости

Два комплексных числа и называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 2.10):

,
=.
Изображающие их векторы симметричны относительно вещественной оси.
Действия над комплексными числами.
Сложение и вычитание производится над числами, записанными в алгебраической форме:

Рис. 2.10. Сопряженные комплексные числа

=, т.е. складываются по отдельности вещественные и мнимые части слагаемых: а = а1+а2, b = b1+b2. Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
    Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части:
+ =.
    Умножение и деление комплексных чисел удобнее всего производить в показательной форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:
                (2.7)
где с= с1 с2, a=a1+a2;
,
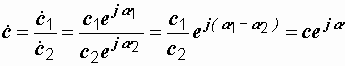где 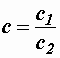, a =a 1 – a 2 .
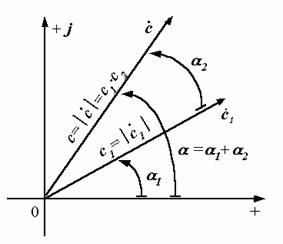
    Что происходит с векторами при перемножении комплексных чисел?
    Изобразим на комплексной плоскости два вектора: 1 – первый сомножитель и – результирующий (рис. 2.11). Последний получается умножением 1 на комплексное число с2е ja2.

На рис. 2.11 мы видим, что при умножении длина вектора возросла в с2 раз, а аргумент увеличился на a2.
Рассматривая комплексное число как вектор, мы приходим к следующему выводу.
При умножении вектора на комплексное число ае ja , вектор растягивается в а раз и поворачивается на угол a.

Рис. 2.11. Перемножение комплексных чисел

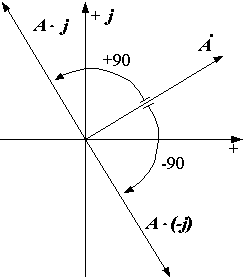
Так как , то при умножении вектора на +- j он поворачивается на угол a 900 (рис. 2.12).

Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа:
x ,
или

Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 = -1

Image4928.gif (2654 bytes)
Рис. 2.12. Умножение вектора на +- j

=
.
При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:

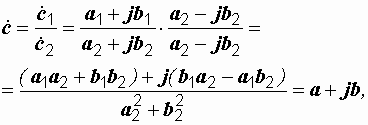
где 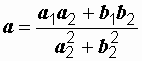; .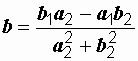
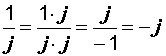