Второй закон Кирхгофа

3. Электрическое напряжение . 2-ой закон Кирхгофа

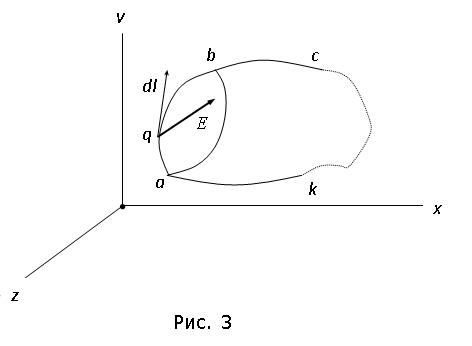
Пусть в электрическом поле `Е заряд q перемещается из точки “a” в точку “b” по некоторой произвольной траектории (рис. 3). Работа сил по перемещению заряда q из точки “a” в точку “b”:

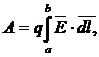
где `Е -напряженность электрического поля [ B/м].

Электрическим напряжением называется физическая величина, равная отношению работы по перемещению заряда из одной точки (а) в другую (b) к величине этого заряда:
.
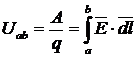Из закона сохранения энергии следует, что при перемещении заряда по произвольному замкнутому контуру, произведенная работа будет равна нулю т.е.

Из этого уравнения вытекают два важных следствия.
1-е следствие: сумма падений напряжений на отдельных участках замкнутого контура равна нулю:

2-ое следствие: напряжение между двумя произвольными точками не зависит от пути интегрирования:
,
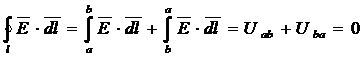откуда следует, что Uab=-Uba.
Независимость напряжения между двумя точками от выбора пути интегрирования позволяет характеризовать электрическое поле некоторой математической функцией ф(x,y, z), называемой потенциалом, разность значений которой в рассматриваемых точках численно равна напряжению между ними:

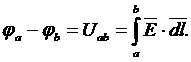
Если положение и потенциал точки ”a” заданы, а точка ”b” является текущей - ”b”(x,y,z), то получим:

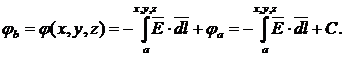
Таким образом, значение потенциала фb в произвольной точке ”b”(x,y,z) зависит от выбора значения потенциала опорной точки фa. В электротехнике принято придавать нулевое значение потенциала точке, связанной с землей.
Рассмотрим замкнутый контур некоторой электрической цепи (рис. 4), при этом путь интегрирования выберем вдоль ветвей контура.

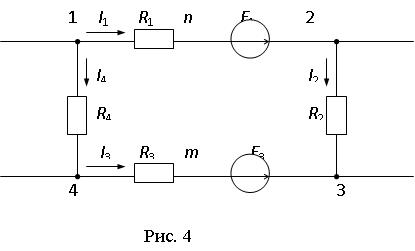
Для 1-й ветви:
U1n=ф1-фn =I1R1 следовательно ф1=фn+I1R1,
U2n=ф2-фn=E1следовательно ф2=фn+E1,
U12=ф1-ф2=фn+I1R1-фn-E1= I1R1- E1.
По аналогии для других ветвей:
U23=ф2-ф3= I2R2 ,
U34=ф3-ф4=-I3R3 +E3,
U41=ф4-ф1=-I4R4 .
Сумма всех напряжений по замкнутому контуру: åU=U12+U23+U34+U41=0, откуда следует, что I1R1 + I2R2 – I3R3 – I4R4 = E1 – E3, или
сумма IR=сумме E - 2-ой закон Кирхгофа.
Формулировка 2-го закона Кирхгофа: в замкнутом контуре электрической цепи или схемы алгебраическая сумма падений напряжений на пассивных элементах контура (сумма IR) равна алгебраической сумме ЭДС (сумма E). Отдельные слагаемые в эти суммы входят со знаком ”+”, если их действие совпадает с направлением обхода контура, и со знаком ”-”, если не совпадает.